지난 게시글에서는 Wage 데이터셋을 활용하여 연령과 임금의 관계, 교육 수준에 따른 임금 변화를 분석해보았습니다. 이번에는 Smarket과 NCI60 데이터셋을 다루며 동일한 과정으로 탐색적 데이터 분석(EDA)을 진행해보겠습니다.
데이터 로드 및 패키지 불러오기
setwd("your_path")
library(ISLR2)
library(dplyr) #이전 게시글에서 설명했습니다! 전 게시글을 참고해주세요
Smarker 데이터셋 살펴보기
names(Smarket)

Smarket 데이터셋은 주식 시장 데이터를 포함한 데이터셋으로,
주가 변화와 관련된 다양한 변수들이 포함되어 있습니다.
데이터셋 안에 변수명들은 year, Lag1~Lag5, volume, Today, Direction 있습니다.
여기서 Lag1~Lag5는 이전 주가 변동률을 의미하며,
예를 들어 Lag1은 전날 주가 변동, Lag2는 2일 전 주가 변동을 나타냅니다.
또한, Direction 변수는 오늘 주가가 전날보다 올랐는지("Up"), 내려갔는지("Down") 를 나타내는 범주형 변수입니다.
Volume은 거래량을 나타내고, Today는 오늘 상승 여부 마지막으로 Direction 최종적으로 올랐는지 내려갔는지 입니다.
여기서 output은 UP 혹은 DOWN 입니다.
데이터 크기 확인
dim(Smarket)

데이터의 차원을 확인해보려면 dim(Smarket) 하시면 됩니다. 1250개의 데이터가 있음을 확인할 수 있습니다.
그 중 데이터의 일부 머리만 보겠습니다
데이터 일부 확인
head(Smarket, n = 6)
Lag가 시간단위의 상승 여부이기 때문에 사실상 year별로 다른 데이터들과 서로 연결되어 있음을 알 수 있습니다.
예를 들어서 3번째 데이터의 Lag2 0.959는 2일 전의 정보입니다. 따라서 2번째 데이터 기준에서는 Lag1에 해당하며 실제로 두번째 데이터의 Lag1은 0.959와 일치합니다. 또 첫번째 데이터 기준에서는 2일후의 데이터 이므로 Today를 확인해보면 0.959로 일치합니다.
연도별 주가 방향(Direction) 분석
addmargins(table(Smarket$Year, Smarket$Direction))
Down, Up의 차이가 수치상으로 큰 차이가 없음을 알 수 있습니다.
주가 변동률과 주가 방향의 관계 분석
par(mfrow = c(1, 3))
boxplot(Smarket$Lag1 ~ Smarket$Direction)
boxplot(Smarket$Lag2 ~ Smarket$Direction)
boxplot(Smarket$Lag3 ~ Smarket$Direction)
증시가 증가하거나 감소한 날에 따라 수익률입니다.
중앙값을 보면 변동의 차이가 없기 때문에 하루 전날 수익으로 오늘의 수익을 예측하는 것은 어려워 보입니다. 사실상 2,3일 전과도 거의 관계가 없다고 생각합니다.
하지만 대략적으로 예측할 수 있습니다. 퍼센트는 현재 60%로 매우 미미하지만 더욱 높일 수 있는 방법이 있습니다.
다음 게시글에서 이를 포스팅 하겠습니다.
Smarket_Data는 Classifier문제에 해당합니다.
NCI60 데이터셋 소개
이제 NCI60 데이터셋을 간략하게 살펴보겠습니다.
이 데이터는 이후 비지도 학습(Clustering, PCA 등) 을 다룰 때 사용할 예정입니다.
str(NCI60)
NCI60$labs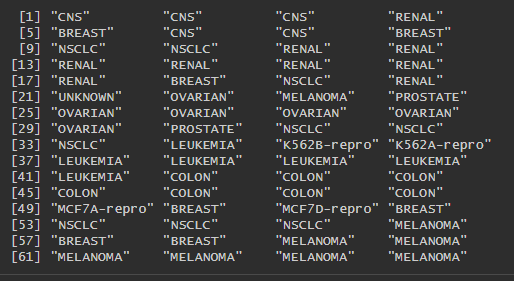
현재 라벨이 공개되어 있지만, 이를 활용하기 보다는 비지도 학습을 통해서 군집화를 해볼 것 입니다.
table(NCI60$labs)
NCI60은 64개의 암세포에 대한 6,830유전자의 발현값으로 구성되어있습니다.
이번 게시글에서는 Smarket 데이터셋과 NCI60 데이터셋을 탐색하며,
각각 주가 변동 예측 가능성 & 유전자 발현 데이터의 구조를 확인해보았습니다.
Smarket 데이터 예측 정확도를 높이는 방법, NCI60 데이터셋을 활용한 비지도 학습(Clustering, PCA)을 포스팅하겠습니다.
'ISLR' 카테고리의 다른 글
| 모수적 방법, 비모수적 방법 (0) | 2025.03.20 |
|---|---|
| MSE (0) | 2025.03.20 |
| ISLR | Basic | 데이터셋 탐색(Wage_Data) (0) | 2025.03.13 |